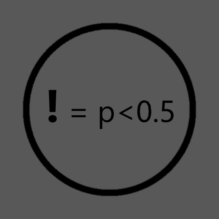Mluvčí předpokládá, že protože data vykazují nějakou statisticky významnou vlastnost, je tato vlastnost významná i prakticky.
Praktická významnost je čistě lidský pojem, který je odpovědí na prostou otázku, jestli je něco možné použít – ať už k nějakému úsudku, či k nějakému rozhodnutí.
Tento faul je často zneužíván v situaci, kdy míra vlivu něčeho je rozdělena do kategorií ANO/NE, ve smyslu lék funguje/nefunguje. Skutečnost, že lék technicky vzato funguje, nutně nemusí znamenat, že funguje natolik, aby mělo smysl ho užívat.
Další podobnou situací bývá moment, kdy je nějaký statistický prvek významný v rámci populace, ale na úrovni jednotlivce je kvůli individuální variabilitě zanedbatelný.
Jedná se o konkrétní případ argumentačního faulu Sloučení společnou vlastností, protože i zde jde o sloučení dvou pojmů – statistická významnost a praktická významnost – na základě povrchní podobnosti.
Příklady
Představme si situaci, kdy zvažujeme kandidáta na pracovní pozici a zároveň chceme, aby měl IQ vyšší než 100. Zjistíme, že lidé pod 175 cm mají v průměru o 2% nižší IQ než lidé nad 175 cm, což je v naší simulované statistice významný rozdíl. Víme ale zároveň, že zhruba dvě třetiny lidí (bez ohledu na výšku) mají IQ někde mezi 85 a 115.
(Tento vztah je fiktivní a je uveden pouze pro účely toho příkladu.)
„Neměli bychom do firmy brát malé lidi. Četl jsem včera v nějaké statistice, že jsou v průměru méně inteligentní.“
Protože je populační rozdíl natolik malý oproti potenciálnímu individuálnímu rozptylu, není praktické tento populační rozdíl při výběru kandidáta vůbec brát v úvahu. Vliv výšky můžeme totiž oproti vlivu náhody úplně zanedbat. Něco jiného by bylo, kdybychom vybírali kandidátů stovky nebo tisíce – v tu chvíli by se náhoda srovnala a rozdíl by začal být relevantní.
Zde spočívá nepraktičnost v rozdílu mezi vlastnostmi souboru a vlastností jedince.
„Náš krém na vyrážku pomáhá v 9 z 10 případů!“
Výrobce krému již neuvádí skutečnost, že zmíněná změna byla většinou viditelná pouze pod mikroskopem a testovaní pacienti změnu vůbec nepocítil. Data však pouze reflektovala, jestli krém fungoval nebo nefungoval – i kdyby to bylo vidět jen pod mikroskopem.
Zde spočívá nepraktičnost ve skutečnost, že test je binární – jsou možnosti jen funguje a nefunguje.
Tento faul totiž krom toho spočívá v tom, že vytvořená statistika využívá matematický model, který přesně neodpovídá realitě, a v tomto případě to vytváří praktický problém s její interpretací a je tudíž zavádějící. Tomuto problému říkáme Matfyzákův omyl.